Canonical Decaying HIT
Decaying homogeneous isotropic turbulence DNS
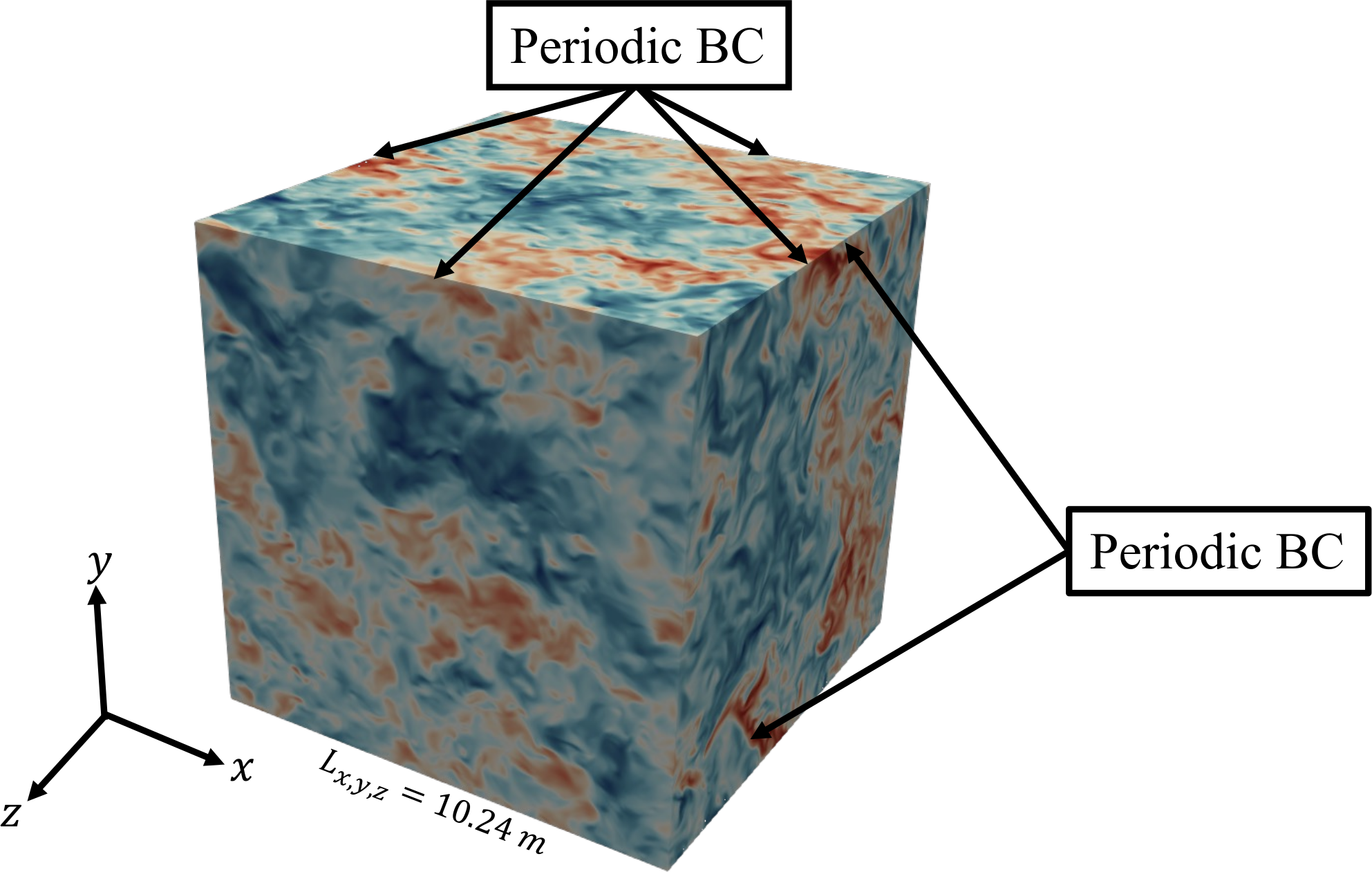
Description
A DNS decaying homogeneous isotropic turbulence simulation is developed by Wang et al. and runs on Tensor Processing Unit (TPU) platform. The Computational Fluid Dynamics (CFD) framework is employed to solve the variable-density Navier-Stokes equation under a low-Mach approximation. The governing equations are discretized using a finite-difference method on a collocated structured mesh within a cubic computational domain with a side length of 10.24 m. The discretization involves a total of N = 2048 grid points in each direction, resulting in a homogeneous grid spacing of Δ = 5 × 10 -3 m. The simulation is initialized with specific turbulence parameters, including an initial Reynolds number Re λ = 309, initial turbulent kinetic energy k0 = 24.42 m2/s2, and initial ratios of Taylor length scale λ0/L = 7.49 × 10-3 and integral length scale l0/L = 2.84 × 10-1. Here, λ and l represent the Taylor length scale and integral length scale, respectively. These initial condition set the stage for investigating the temporal evolution and decay characteristics of homogeneous isotropic turbulence within the computational domain.
Quick Info
- Contributors: Qing Wang, Shantanu Shahane, Yifan Chen
- Nx = 2040, Ny = 2040, Nz = 2048, Nɸ = 4
- DOI
- .bib
Links to different cases
| ID | Conditions | Size (GB) | Links |
|---|---|---|---|
| 0 | TKE = 25.8844, ε = 65.7053 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 1 | TKE = 21.2626, ε = 39.3486 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 2 | TKE = 17.1823, ε = 37.9396 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 3 | TKE = 13.7007, ε = 30.2196 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 4 | TKE = 9.3180, ε = 16.4062 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 5 | TKE = 5.8251, ε = 7.4214 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 6 | TKE = 3.4790, ε = 3.2468 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 7 | TKE = 1.9369, ε = 1.2832 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 8 | TKE = 1.0627, ε = 0.5080 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 9 | TKE = 0.6658, ε = 0.2389 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 10 | TKE = 0.4521, ε = 0.1295 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 11 | TKE = 0.3339, ε = 0.0789 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 12 | TKE = 0.2596 ε = 0.0518 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 13 | TKE = 0.2119, ε = 0.0375 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 14 | TKE = 0.1765, ε = 0.0283 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 15 | TKE = 0.1488, ε = 0.0215 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 16 | TKE = 0.1268, ε = 0.0167 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 17 | TKE = 0.1090, ε = 0.0131 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 18 | TKE = 0.0953, ε = 0.0107 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |
| 19 | TKE = 0.0843, ε = 0.0089 | 120 |
KaggleV, KaggleP info.jsonV, info.jsonP |