Forced HIT

Forced Homogeneous Isotropic Turbulence DNS with 3 Passive Scalars

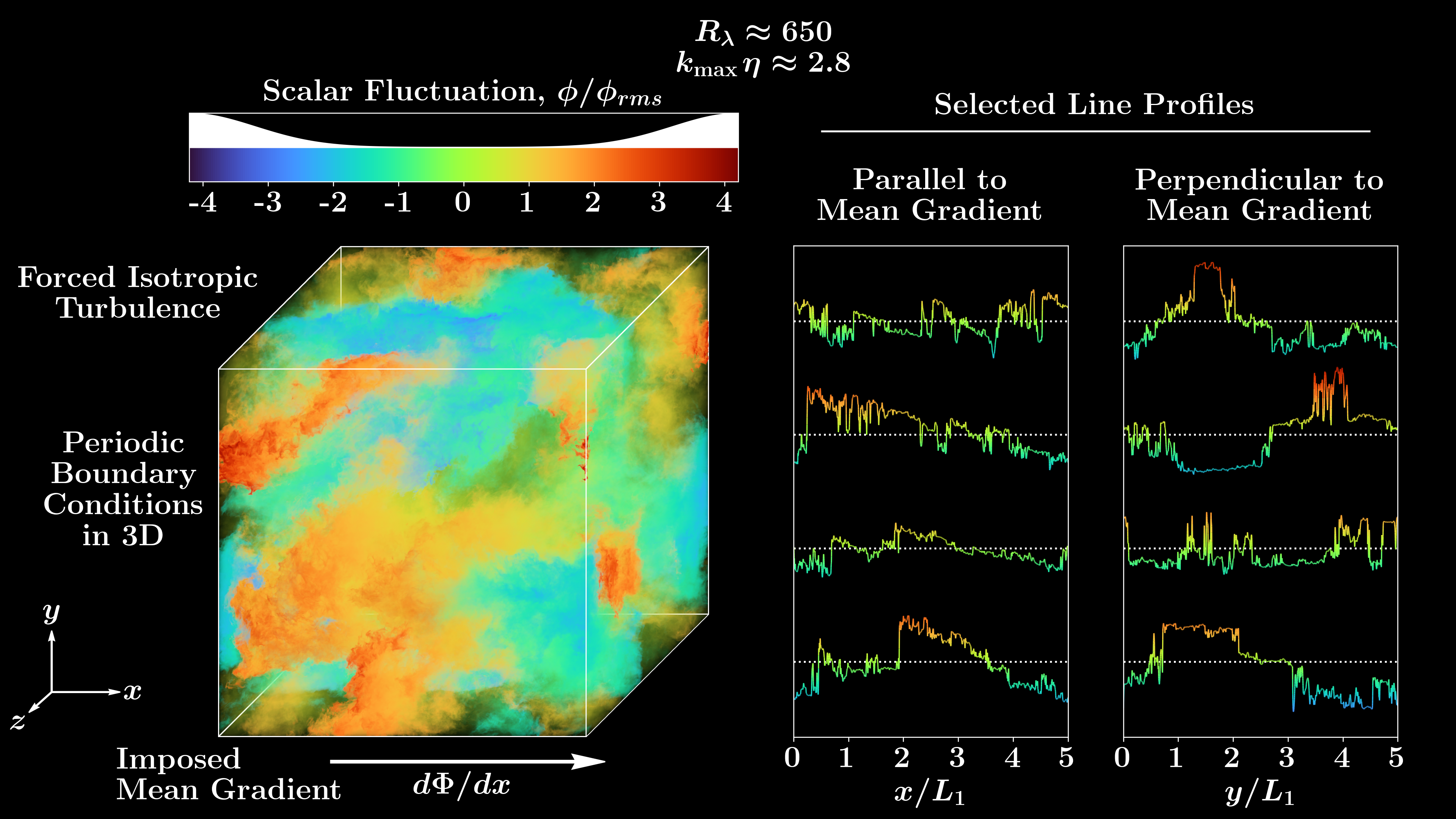
Description

These snapshots are from a series of Direct Numerical Simulations (DNS) of passive scalar mixing in three-dimensional homogeneous isotropic turbulence, at grid resolution up to $16384^3$ [1], performed using the exascale supercomputer named Frontier at Oak Ridge National Laboratory. The velocity fluctuations evolve according to the incompressible Navier-Stokes equations, while the scalar fluctuations follow an advection-diﬀusion equation, with a source term representing an imposed mean scalar gradient. The numerical methods employed are standard Fourier pseudo-spectral in space, second order in time, with aliasing errors controlled by a combination of phase shifting and truncation [2]. The velocity field is forced by keeping the values of the energy spectrum in the three lowest wavenumber shells constant [3].

The simulations begin from previously evolved velocity fields and are first run at a modest resolution of $k_{max}\eta \approx 1.4$ (where $k_{max} = \sqrt 2 N/3$ is the highest wavenumber resolved on an $N^3$ grid and $\eta$ is the Kolmogorov length scale) until the scalar fields reach statistical stationarity. The grid is then refined to a higher resolution of $k_{max} η \approx 2.8$, and the simulation proceeds until the smallest scales fully adjust. Snapshots at this highest resolution have been collected for Taylor-scale Reynolds numbers $Re_\lambda \approx 390, 650, 1000 \text{ and } 1600$. The Schmidt number is $1.0$ in all cases. Each snapshot captures the complete flow field — including velocity, pressure, and three passive scalars — at a single instant in time. The three scalars are each subjected to a uniform mean gradient along a diﬀerent coordinate direction.

Quick Info

Contributors: P.K Yeung, Daniel Dotson
N_ɸ = 4 + 3
DOI
.bib

Links to different cases

ID	Re$_{\lambda}$	Grid	Size (GB)	Links
0	390	2048³	225`	Kaggle_VP, info.json_VP, Kaggle_Y, info.json_Y
1	650	4096³	1.8 TB	Kaggle_P₁, info.json_P₁, Kaggle_P₂, info.json_P₂, Kaggle_U₁, info.json_U₁, Kaggle_U₂, info.json_U₂ Kaggle_V₁, info.json_V₁, Kaggle_V₂, info.json_V₂ Kaggle_W₁, info.json_W₁, Kaggle_W₂, info.json_W₂ Kaggle_{Y_1,1}, info.json_{Y_1,1}, Kaggle_{Y_1,2}, info.json_{Y_1,2} Kaggle_{Y_2,1}, info.json_{Y_2,1}, Kaggle_{Y_2,2}, info.json_{Y_2,2} Kaggle_{Y_3,1}, info.json_{Y_3,1}, Kaggle_{Y_3,2}, info.json_{Y_3,2}

References

[1] D. L. Dotson, P. K. Yeung, and K. R. Sreenivasan. A Study of passive scalar turbulence at high Reynolds numbers enabled by exascale computing. Bull. Am. Phys. Soc. https://meetings.aps.org/Meeting/DFD24/Session/R37.00003, 2024.
[2] R. S. Rogallo. Numerical experiments in homogeneous turbulence. NASA TM 81315, NASA Ames Research Center, Moﬀett Field, CA., 1981.
[3] D. A. Donzis and P. K. Yeung. Resolution eﬀects and scaling in numerical simulations of passive scalar mixing in turbulence. Physica D, 239:1278–1287, 2010.