Supercritical Homogeneous Isotropic Turbulence DNS

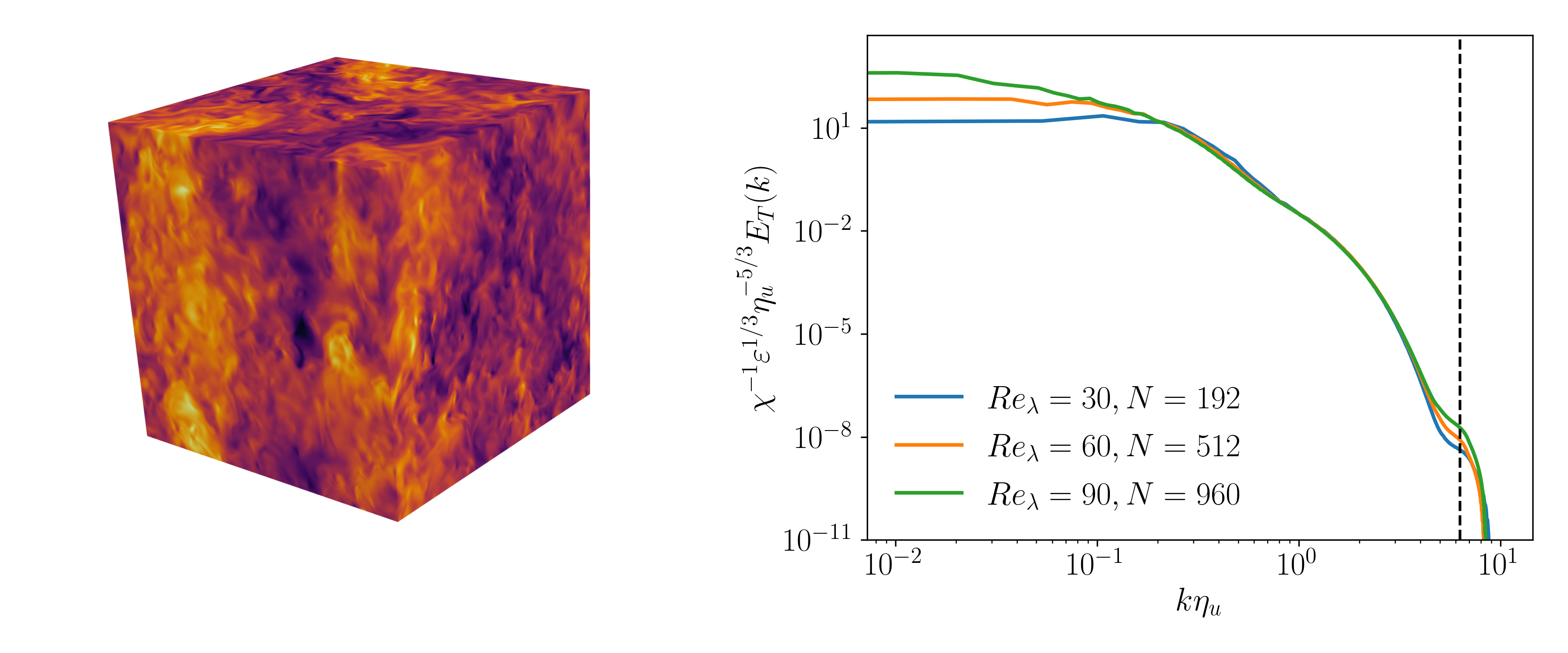
Image 1

Description

This dataset contains snapshots from Batchelor-resolved direct numerical simulations (DNSs) of homogeneous isotropic turbulence (HIT) of supercritical carbon dioxide (\(\text{CO}_2\)). The bulk pressure is fixed at $P_0/P_c = 2$, where $P_c = 7.38 \text{MPa}$ is the critical pressure of \(\text{CO}_2\). The bulk temperature $T_0$ corresponds to the pseudo-boiling point at this pressure, identified by the maximum in the specific isobaric heat capacity $c_P$. At these conditions, the bulk Prandtl number is $Pr_0 = \mu_0c_{P_0}/\kappa_0 \approx 2.17$, where the subscript $0$ for the thermophysical variables denotes properties evaluated at the reference thermodynamic state {$P_0$,$T_0$}. Due to the higher-than-unity Prandtl number, thermal fluctuations persist at sub-Kolmogorov scales.

Three Taylor Reynolds numbers are considered: $Re_\lambda \approx 30,\ 60, \text{ and } 90$. The computational domain is a triply periodic cube of side length $L = 5.5 L_0$, where $L_0$ is the integral length scale. The corresponding grids contain $N = 192,\ 512, \text{ and } 960$ interior points per direction, re- spectively. The grid resolutions satisfy $k_{max}\eta_T \approx 3.18–3.45$, where $k_{max} = \pi N/L$ is the maximum resolved wavenumber, $\eta_T = \eta_u/\sqrt{Pr_0}$ is the Batchelor scale, and $\eta_u = [(\mu_0/\rho_0)^3/\epsilon_0]^{1/4}$ is the Kolmogorov scale. The numerical grid includes two additional ghost points in each direction, which are used to impose the boundary conditions. Accordingly, the mesh coordinates in the i-th direction are then given by $x_i = −\Delta h/2 + j\Delta h$ $j = 0,…,N + 1$, where $\Delta h = L_{box}/N$ denotes the uniform grid spacing.

The equations of fluid motion are computationally solved using the in-house flow solver RHEA [1]. Spatial operators are treated using second-order central-differencing schemes, and time-advancement is explicitly performed by means of a third-order strong-stability pre-serving (SSP) Runge-Kutta approach [2]. The Kennedy-Gruber-Pirozzoli (KGP) splitting is adopted for the convective terms extended to high-pressure transcritical fluids turbulence [3], ensuring kinetic-energy preservation by convection. This numerical framework provides stable computations without the need of any form of artificial dissipation or stabilization procedures. To accurately capture the rapid variations in thermophysical properties across the pseudo-boiling line, thermodynamic properties are evaluated using the Peng–Robinson equation of state [4], while transport properties are determined from the correlations proposed by Chung et al. [5,6]. Turbulence is sustained using a solenoidal linear forcing following Watanabe et al. [7], which maintains statistically stationary conditions by enforcing a target root-mean-square velocity fluctuation $u_0$ and a prescribed dis- sipation rate per unit of volume $\rho_0\epsilon_0$, while conserving total energy $E$. Flow variables $(\rho, u, v, w, P, T)$ and thermophysical properties $(\mu, \kappa, c_p)$ are stored at a frequency corresponding to 5 snapshots per characteristic time $t_0$. This results in weak temporal correlation between consecutive snapshots. For the cases with $Re_\lambda \approx 30,\ 60, \text{ and } 90$, a total of $709,\ 40, \text{ and } 12$ snapshots, respectively, are included in the dataset. Further information can befound in Martin and Jofre [8].

Quick Info

  • Contributors: David Martin, Lluis Jofre

  • Nɸ = 5 + 4

  • DOI
  • .bib
Case Re$_{\lambda}$ Grid Size (GB) Links
1 30 194×194×194 174 Kaggle, info.json
2 60 514×514×514 183 Kaggle, info.json
3 90 962×962×962 360

References

[1] L. Jofre, A. Abdellatif, and G. Oyarzun, “RHEA - an open-source Reproducible Hybrid-architecture flow solver Engineered for Academia,” J. Open Source Softw. 8, 4637 (2023).
[2] S. Gottlieb, C. W. Shu, and E. Tadmor, “Strong stability-preserving high-order time discretization methods,” SIAM Review 43, 89–112 (2001).
[3] M. Bernades, L. Jofre, and F. Capuano, “Kinetic-energy- and pressure-equilibrium-preserving schemes for real-gas turbulence in the transcritical regime,” J. Comput. Physics 493, 112477 (2023).
[4] D. Y. Peng and D. B. Robinson, “A new two-constant equation of state,” Ind. Eng. Chem. Fundam. 15, 59–64 (1976). [5] T. H. Chung, L. L. Lee, and K. E. Starling, “Applications of kinetic gas theories and multiparameter correlation for prediction of dilute gas viscosity and thermal conductivity,” Ind. Eng. Chem. Fund. 23, 8–13 (1984).
[6] T. H. Chung, M. Ajlan, L. L. Lee, and K. E. Starling, “Generalized multiparameter correlation for nonpolar and polar fluid transport properties,” Ind. Eng. Chem. Fund. 27, 671–679 (1988).
[7] T. Watanabe, K. Tanaka, and K. Nagata, “Solenoidal linear forcing for compressible, statistically steady, homogeneous isotropic turbulence with reduced turbulent Mach number oscillation,” Phys. Fluids 33 (2021), 10.1063/5.0062596.
[8] D. Mart ́ın and L. Jofre, “High-fidelity database of supercritical homogeneous isotropic turbulence in the pseudo-boiling region,” Sci. Data 12 (2025), https://doi.org/10.1038/s41597-025-05693-3.

Updated: